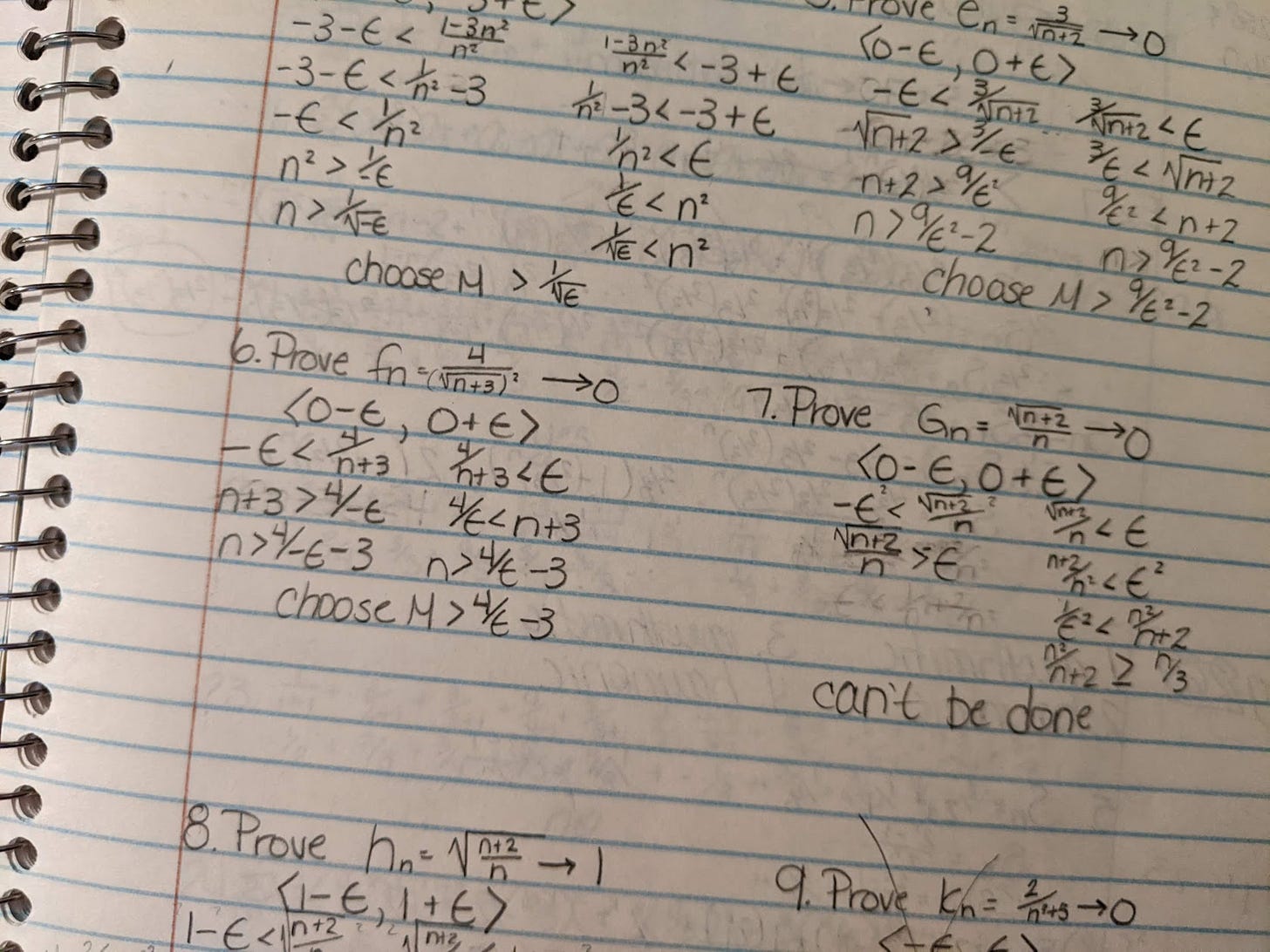We all long for Q.E.D.

This is a ridiculously long post.

From my high school senior math (not geometry) notebook.

Q.E.D. = quod erat demonstrandum (“that which was to be demonstrated”)

A few years after college, while working the night shift at a postal processing facility, a former co-worker came to me and asked if I’d help her son pass geometry.

“He’s failing and he’ll be ineligible,” she told me. “The teacher said if he could pass his final he would pass the class.”

Apparently the teacher was nice, but her son was struggling to understand how the math was being taught. Though it had been years since I’d taken geometry (tenth grade, in fact), I agreed.

I really liked geometry. It made sense.

Given this, prove this. Build on what you’ve already proven. Make a statement, make a reason for the statement, and step by step, complete the proof.

I agreed to help.

The mom got a copy of her son’s geometry textbook from the school, and I would take it and a notebook along to work. During my 3 a.m. lunchbreak, I’d spend the time methodically working through the examples for each chapter on the left side of the paper while writing an explanation for what I was doing on the right side. Then, after work, I’d get those pages over to her and head home.

I was a bit nervous. I was rusty, and math isn’t my strong point. (Art major here.) I wanted the kid to pass.

He did.

“He said he finally understands how to do it!” the mom told me. I used the older methods from my excellent high school math teacher, and that made sense to him it seemed.

Geometry, like much of the low-level math I’ve been exposed to, has a methodology that feels very satisfying when you get to the answer. But geometry was even more so; it felt like solving mysteries to solve more mysteries, and I do love a mystery.

If you don’t mind an art major taking a sloppy swing at things, it goes a bit like this:

1. You state a hypothesis you believe, or intend to prove, is true. Using postulates and proven theorems, you reach a conclusion to find out if the hypothesis is true. If I can prove a hypothesis, someone else should be able to do so, too.

2. Postulates are statements we assume are true, without any proof. They don’t need to be proven, and you can use them in your proof of your hypothesis. In geometry, for example, you could say that when you connect two points you have a segment. It’s a visibly true statement.

3. Theorems consist of hypothesis and conclusions. Theorems are statements we can prove to be true using postulates or already-proven theorems through a logical progression. Like Robert Frost’s poem tells us, way leads on to way, and we can get to the final proof through reasoning.

4. Watch out for lemmas. Sometimes you find yourself working through a theorem and stumble upon a lemma, which is an unproven theorem that must be proven before you can use it any further towards your original proof.

5. Postulates and theorems are the key to proof. How you think about them depends on if you’re looking for a definition, if you’re referencing them in regards to a proof, or if you’re referencing them in regards to something that needs to be proven.

6. At the end, you’ve proven what you said was true. When you get to the conclusion having proved your hypothesis correct, you get that glorious moment of being able to use QED (or just ▢), solid in knowing your proof can withstand any argument.

Again, art major. What I’m doing here is fleshing out some verbal postulates of sorts, because I’m about to venture further in this blog post and will need them to reach my conclusion.

We could all—myself included—do with a refresher course on thinking this way.

True, most things aren’t as perfectly tidy; some involve human beings and emotions and lack the perfectly unarguable proven conclusion. Most things aren’t so black and white and what someone sees as a postulate or proven theorem, another might disagree. History, for example, has the facts of what happened, but the context and the why behind the what is incredibly complex.

Still, the elements and the basic structure can be used to lead you to a pretty decently proven point—or determine if something is believable—even if it’s not a 100 percent right triangle. If we took that approach, every piece of information that crossed our screens, landed in our ears, or lifted up off the page would get a check.

No, not an infamous “fact check” of social media fame. Just a check.

What are the postulates? What are we mistaking as a postulate that’s actually an unproven theorem? Is someone using a lemma as if it were proven? What’s the hypothesis? Are the postulates even related to that hypothesis?

For example, around February 19, images were spreading on social media of various lines of semi-trucks purported to be in Ohio and the Pacific Northwest. People said these were part of the People’s Convoy, the American version of the Canadian convoy.

Is it a line of trucks? Yes.

Is it in Ohio? I can’t tell from the photo.

Is it the People’s Convoy? I don’t know.

Who took the photo? No idea.

<Click Share Anyway>

The People’s Convoy wasn’t starting until February 23. Sure, it could have been that these were other truckers doing this themselves, but it wasn’t the right kind of weather for the place the photo was allegedly taken. There was no photo credit to indicate who had taken the image.

With an image, you could at least do an internet search to find out if it’s been used before. You can zoom in and see if it looks like pixels are wonky and there’s evidence of alteration. But that takes time.

What’s our problem today?

We don’t recognize lemmas. We’re too lazy or busy to prove them when we do. We mistake an interesting hypothesis from an interesting person as a postulate. Or we go right from hypothesis to conclusion. We all do this, because we’re overloaded with so much information every day that we have to take shortcuts to process it. (Suggestion: reduce your incoming information.)

I don’t blame people, completely, because this is what’s modeled for them.

Our news media does not prove things well. In fact, they’re at the horrific point that they don’t even hypothesize well. A hypothesis arises when you take note of some data or a situation, and too often our news sources are busy looking away.

Being a researcher and investigator takes time and the right connections; it’s knowing who is qualified to verify each different type of information due to their experience or knowledge. (See also: the end of Dan Rather’s career, and Microsoft Word.)

Since we average joes without connection or expertise generally can’t verify things easily, we have to trust sources. We have to trust someone is verifying the who, what, when, where, and why.

We have no shortage of sources, but too many are bought and paid for. And we also have the problem of not knowing how to separate message from messenger and that even a broken clock is right twice a day.

Take, for example, this beauty floating around on social media:

Some sources are way off in tinfoil hat land, others are corrupted. So what do you do when, once in a while, they get things right? Can you sift that out?

If Satan supports something, I’ll give it a hard pass. Other than that, I need to prayerfully consider, be cautious, be wary of hot takes, and revert to looking for ways to prove whatever I can, even tiny things (like emotionally manipulative images attributed to events). If I can’t be sure, it’s best to step back and wait and see what information comes out.

Because, when we’re faced with information, we want to organize it so we can understand and trust it. We all want Q.E.D. (“that which was to be demonstrated”).

Oh, That Special, Secret Knowledge

On the flip side, if I’m going to talk about QED, I have to talk about Q.

Q, the unknown entity assuring Trump supporters to trust the plan, and that “where we go one, we go all” (WWG1WGA).

I can’t define what Q is/was. There’s no point in doing an internet search for explanation, either, because the outsiders don’t quite get it right (referring to the movement as Qanon), and the insiders are secretive and sort of exclusive. You either have to dive in and get a sense, or not bother.

I tried to figure it out in 2019 and 2020. I didn’t venture too far into the 4chan or 8chan arena, where the Q posts (“drops”) were posted. I don’t even like reddit; I’m not going into the chans. I finally downloaded an app that updated you whenever there was a new post by the mysterious Q. Then people would chime in with Q “proofs” in the chans or on Twitter, proofs which were far from actual proofs and more akin to looking at the clouds and seeing shapes in the randomness. “Look at the string of numbers, it matches a date when such and such happened. Trump used this word and phrase on Twitter and Q used that same phrase last year on the reverse date. Compare this time stamp with the metadata on that photo.”

Stuff like that.

Not proofs. Correlations, coincidences, associations, or manipulations, but not a proof as we are defining it here. If it was a proof, all of the promises made by Q would have happened.

We don’t like randomness, so we look for patterns. We like to solve mysteries, find some order in the meaningless chaos, and feel like we have special inside knowledge. Most people fall into these categories someplace. If we didn’t, we wouldn’t find gossip so tasty and God wouldn’t have to remind us in his word that there are mysteries that belong only to him, and if he choses to reveal them, he’ll do so in his time. No need for us to do any astrological hanky panky or political cryptic mumbo jumbo to get a jump on the game. Read God’s Word, and talk to him constantly.

Yet the tendency is still there, and it makes nearly all of us an easy mark for the confidence man. How does he con you? He gains your confidence. He lets you in on the secret, the amazing deal, the incredible 12%+ investment opportunity others don’t know about. He makes you feel special, chosen, because you get to know something big while others don’t.

I gave up on Q after about a month. I found it about as annoying as the Star Trek: TNG character named Q. Who has the time to try to find meaning in gibberish, in a photo of a pen on paper supposedly taken in the Oval Office, or the hidden meaning behind the time displayed on a watch supposedly taken on Air Force One? If people spent that much time reading their Bible, what a big difference the world would see.

After the election, over on the Gab social network, Q was everywhere. Q popped up in profile names and in every graphic. The number 17 (the letter Q is the the 17th letter in the alphabet) was holy, practically. They were talking about owl patterns at the capitol and trusting the plan and something special in March.

But Q was addictive, still has devotees—many are good, patriotic people, some are less so—and that level of success spawned what I call cryptic copycats.

There’s a market to be had, some people discovered, in selling mystery and a hope of big returns and secret knowledge and being “awake” to the truth of the reason behind all the evil in the world. (See also: Satan, and also, every secret society ever.)

I’m a writer. While I can get verbose, such as this ridiculously long blog post, I’m a big fan of speaking plainly, particularly if you’re trying to impart specific and actionable information instead of philosophically rambling about geometry proofs. These cryptic folks take a different approach.

So now we enter the weird part of the post.